반응형
DFS는 그래프(Graph)를 탐색하는 방법입니다.
그래프란, 정점(node)과 그 정점을 연결하는 간선(edge)으로 이루어진 자료구조를 말합니다.
코딩 테스트에서 BFS와 단골로 나오는 개념입니다.
DFS 깊이 우선 탐색(Depth-First Search)
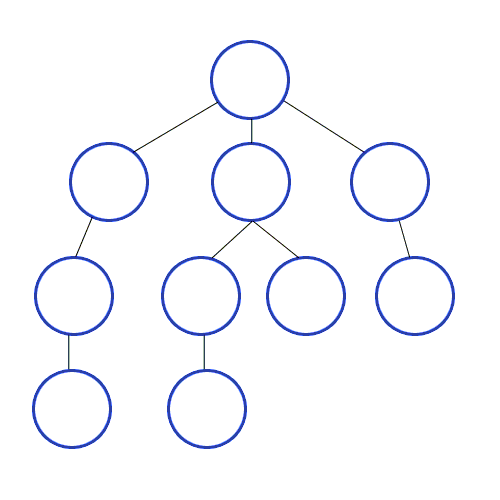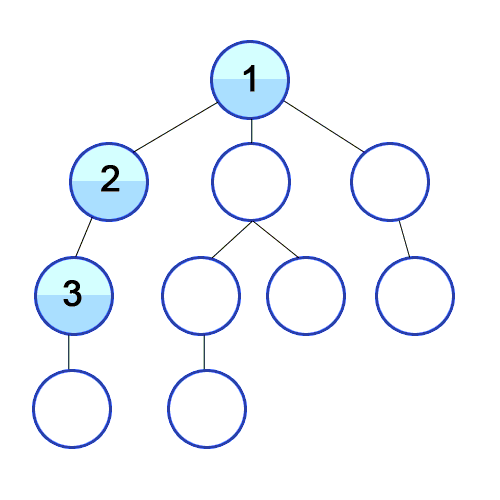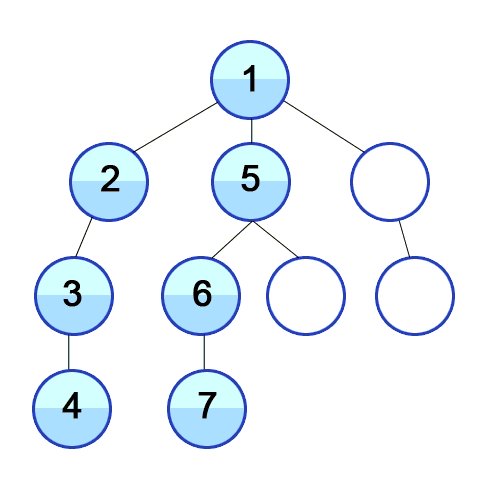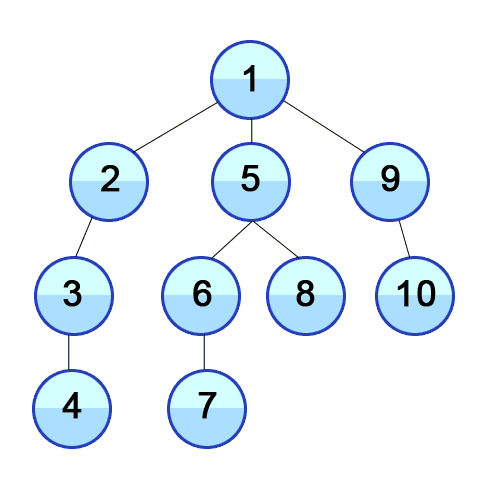
정의 : 루트 노드(혹은 다른 임의의 노드)에서 시작해서 다음 분기(branch)로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법을 말합니다.
자기 자신을 호출하는 순환 알고리즘이기 때문에 재귀 함수나 스택을 가지고 구현합니다. 이때 주의 사항은 어떤 노드를 방문했었는지 여부를 반드시 검사해야 합니다.
📘 Pseudo Code
/**
1. 노드이 갯수 만큼 방문 여부를 위한 배열 생성 후 false로 초기화 (visit 배열)
2. 루트 노드부터 DFS 탐색 시작
**/
DFS(G, u)
u.visited = true
for each v ∈ G.Adj[u]
if v.visited == false
DFS(G,v)
/**
1. 현재 탐색하는 노드가 제일 깊은 노드라면 return
2. 아니면 반복문을 통해 방문하지 않은 노드 DFS 탐색
**/
init()
For each u ∈ G
u.visited = false
For each u ∈ G
DFS(G, u)
📘 코드 - 재귀 구현 방식(백준 2606번 - 바이러스)
var n : Int = 0
var m : Int = 0
var graph = Array(101){Array(101){0}}
var visit = Array(101){0}
fun main(args : Array<String>) = with(Scanner(System.`in`)) {
var a : Int
var b : Int
n = nextInt()
m = nextInt()
for(i in 0 until m){
a = nextInt()
b= nextInt()
graph[a][b] = 1
graph[b][a] = 1
}
dfs(1)
println(visit.filter { it==1 }.size-1)
println(visit.toList())
}
fun dfs(x : Int){
visit[x] = 1
for(i in 1..n){
if(visit[i] ==1 || graph[x][i] ==0) continue
dfs(i)
}
}
보통 DFS는 아래와 같은 문제 유형에서 주로 사용이 됩니다.
- 그래프의 모든 정점을 방문하는 문제
- 경로들을 특징해서 저장해야 하는 문제
- 검색 대상의 그래프가 많이 큰 경우
- 사이클이 존재하는 경로를 찾는 경우
DFS는 끊임없이 깊이 탐색하기 때문에 그래프가 깊어지면 찾는데 탐색하는데 시간이 오래 걸릴 수 있습니다. 그래서 지금의 경로가 해가 될 것 같지 않으면 그 경로를 중단하고 상위의 노드로 이동해 다시 탐색하는 방법이 있는데 이를 백트래킹 알고리즘이라고 합니다. (예제 - 프로그래머스 소수 찾기)
반응형
'컴퓨터 공학 > 알고리즘' 카테고리의 다른 글
| [알고리즘 / Kotiln] 프로그래머스 - 수식 최대화 (2020 카카오 인턴십) (0) | 2022.02.08 |
|---|---|
| [알고리즘] BFS(Breadth-First Search) - 너비 우선 탐색 (0) | 2021.12.13 |
| [알고리즘 / Kotlin] 프로그래머스 - 큰 수 만들기 (0) | 2021.11.22 |
| [알고리즘 / JAVA] 까먹지 않기 위한 기본 정렬 알고리즘 (0) | 2021.11.10 |
| [알고리즘 / Kotlin] 프로그래머스 - (10주차)교점에 별 만들기 (0) | 2021.10.17 |




댓글